Markov-Chain Model¶
The evolution of the Pairwise Annihilation protocol is described by a continuous-time Markov chain with state space $S = \mathbb{N}^2$.
Its state-transition rates are:
\begin{equation}
\begin{split}
\qquad \qquad \qquad Q\big( (A,B) \,,\, (A+1,B) \big) & = \mu A\\
Q\big( (A,B) \,,\, (A,B+1) \big) & = \mu B\\
Q\big( (A,B) \,,\, (A-1,B-1) \big) & = \delta A B
\end{split}
\end{equation}
Note that the death transition $(A,B) \to (A-1,B-1)$ has rate zero if $A=0$ or $B=0$.
Both axes $\{0\}\times\mathbb{N}$ and $\mathbb{N}\times\{0\}$ are absorbing, and so is the state $(A,B)=(0,0)$.
This chain is regular, i.e., its sequence of transition times is unbounded with probability $1$.
Indeed, as we will show, the discrete-time chain reaches consensus with probability $1$, from which time on the chain is equal to a linear pure-birth process, which is regular.
The corresponding discrete-time jump chain has the same state space $S=\mathbb{N}^2$ and the state-transition probabilities
\begin{equation}
\begin{split}
P\big( (A,B) \,,\, (A+1,B) \big) & = \frac{\mu A}{\mu(A+B) + \delta AB}\\
P\big( (A,B) \,,\, (A,B+1) \big) & = \frac{\mu B}{\mu(A+B) + \delta AB}\\
P\big( (A,B) \,,\, (A-1,B-1) \big) & = \frac{\delta AB}{\mu(A+B) + \delta AB}
\end{split}
\end{equation}
if $A>0$ or $B>0$.
The axes as well as state $(A,B)=(0,0)$ is absorbing, as in the continuous-time chain.
As a convention, we will write $X(t)$ for the state of the continuous-time process $X$ at time $t$, and $X_k$ for the state of the discrete-time jump process after $k$ state transitions.
The time to reach consensus is the earliest time $T$ such that $A(T)=0$ or $B(T)=0$.
Time to Reach Consensus¶
In this section we prove the bounds on the time to reach consensus, both in expected time and with high probability.
For that, we will employ a coupling of the Pairwise Annihilation protocol Markov chain with a single-species birth-death process.
We show that the Pairwise Annihilation protocol reaches consensus when the single-species process reaches its extinction state and then bound this time in the single-species process.
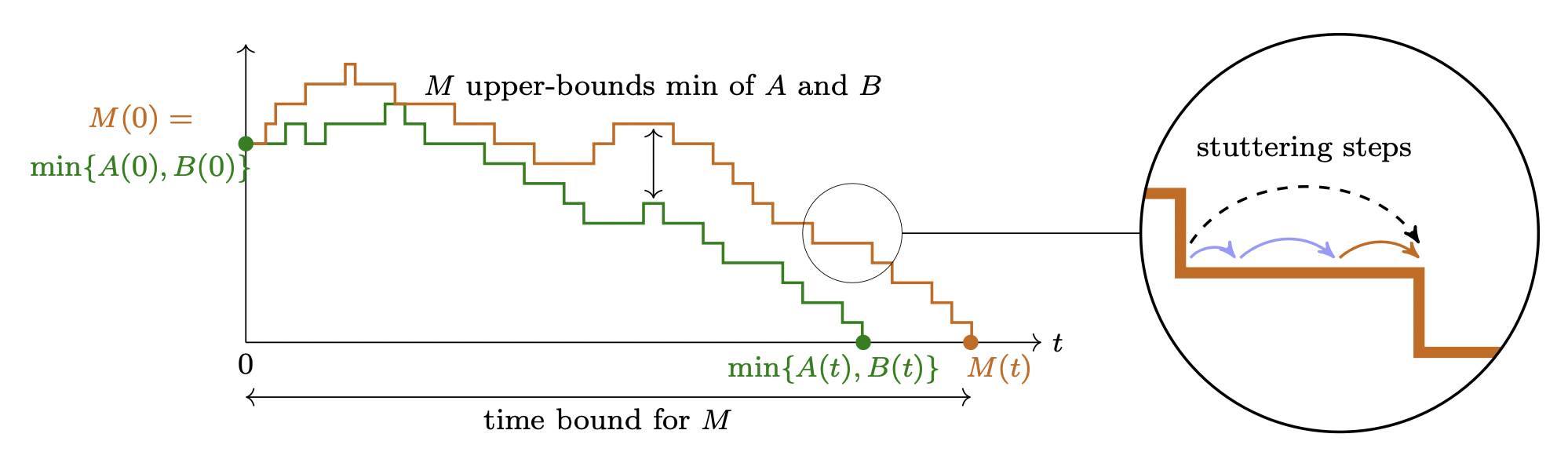
Idea of the proof: Construction of a continuous-time coupling of the Pairwise Annihilation protocol and the single-species birth-death M chain.
Stuttering steps are mapped to effective steps.
An execution of the coupling process fulfills the deterministic guarantee $\min\{A(t),B(t)\}\leq M(t)$ for all times $t\geq0$.
From the coupling it follows that
$\mathbb{P}\bigr(M(t)=0\bigl) \leq \mathbb{P}\bigr(A(t)=0 \vee B(t)=0\bigl)$ for the uncoupled processes.
The time until consensus then follows from the time until extinction in the M chain.
We denote the single-species process by $M(t)$.
It is a birth-death chain with state space $S=\mathbb{N}$ and transition rates $Q(M,M+1) = \mu M$ and $Q(M,M-1) = \delta M^2$.
State $0$ is absorbing.
Note that the death rate $\delta M^2$ depends quadratically on the current population $M$, and not linearly like the birth rate $\mu M$.
The reason is that we want $M(t)$ to bound the minimum of the populations $A(t)$ and $B(t)$ and that the death transition in the Pairwise Annihilation protocol is quadratic in this minimum.
We will crucially use the fact that $\mathbb{P}\bigr(M(t)=0\bigl) \leq \mathbb{P}\bigr(A(t)=0 \vee B(t)=0\bigl)$ for all times $t$.
This, together with a bound on the time until $M(t)=0$, then gives a bound on the time until consensus in the Pairwise Annihilation protocol chain.
Continuous-time coupling¶
The coupling is defined as follows.
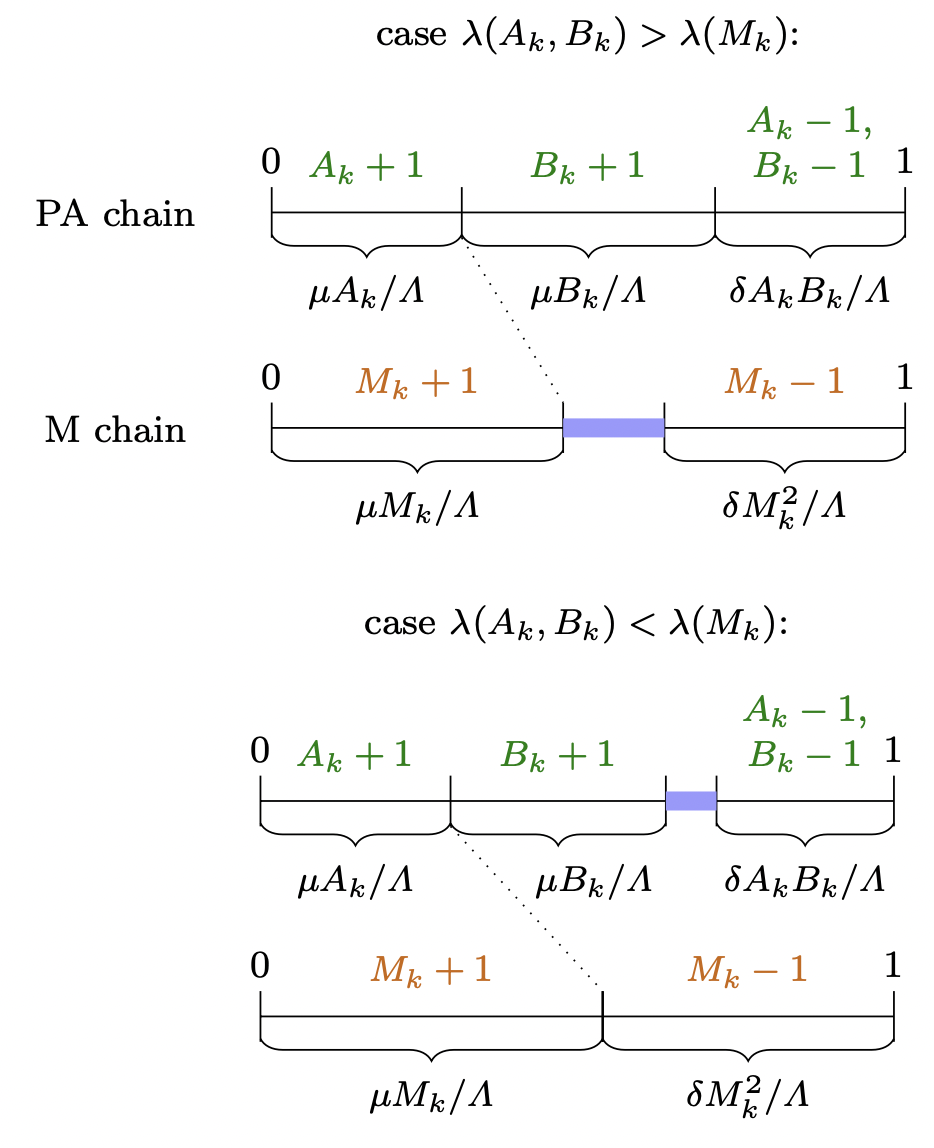
For sequences $(\xi_k)_{k\geq1}$ of i.i.d. (independent and identically distributed) uniform random variables in the unit interval $[0,1)$ and $(\eta_k)_{k\geq1}$ of i.i.d. exponential random variables with normalized rate $1$, we define the coupled process $(A(t),B(t),M(t))$ as follows.
Initially, $M(0) = \min\{A(0),B(0)\}$.
For $k \geq 0$, the $(k+1)$th transition happens after time $\eta_k/\Lambda(A_k,B_k,M_k)$ where
$\Lambda(A,B,M) = \max\{\lambda(A,B),\lambda(M)\}$
is the maximum of the sums of transition rates of the individual chains in states $(A,B)$ and $M$, respectively, i.e., $\lambda(A,B)=\mu(A+B)+\delta AB$
and
$\lambda(M) = \mu M + \delta M^2$.
The new state $(A_{k+1},B_{k+1},M_{k+1})$ of the coupled chain is then determined by the following update rules.
The state $(0,0,0)$ is absorbing.
Otherwise, if $A_k \leq B_k$, then:
\begin{equation}
(A_{k+1},B_{k+1})=
\qquad \begin{cases}
(A_k+1,B_k) \quad & \text{if } \xi_{k+1} \in \left[ 0 \,,\, \frac{\mu A_k}{\Lambda(A_k,B_k,M_k)} \right)\\
(A_k,B_k+1) & \text{if } \xi_{k+1} \in \left[ \frac{\mu A_k}{\Lambda(A_k,B_k,M_k)} \,,\, \frac{\mu A_k+\mu B_k}{\Lambda(A_k,B_k,M_k)} \right)\\
(A_k-1,B_k-1) & \text{if } \xi_{k+1} \in \left[ 1 - \frac{\delta A_k B_k}{\Lambda(A_k,B_k,M_k)} \,,\, 1 \right)\\
(A_k,B_k) & \text{otherwise}
\end{cases}
\end{equation}
If $A_k > B_k$ then the roles of $A_k$ and $B_k$ in the above equation are exchanged.
The update rule for $M_{k+1}$ is:
\begin{equation}
M_{k+1}¶
\begin{cases}
M_k + 1 & \text{if } \xi_{k+1} \in \left[ 0 \,,\, \frac{\mu M_k}{\Lambda(A_k,B_k,M_k)} \right)\\
M_k - 1 & \text{if } \xi_{k+1} \in \left[ 1 - \frac{\delta M_k^2}{\Lambda(A_k,B_k,M_k)} \,,\, 1 \right)\\
M_k & \text{otherwise}
\end{cases}
\end{equation}
Analysis for time until consensus¶
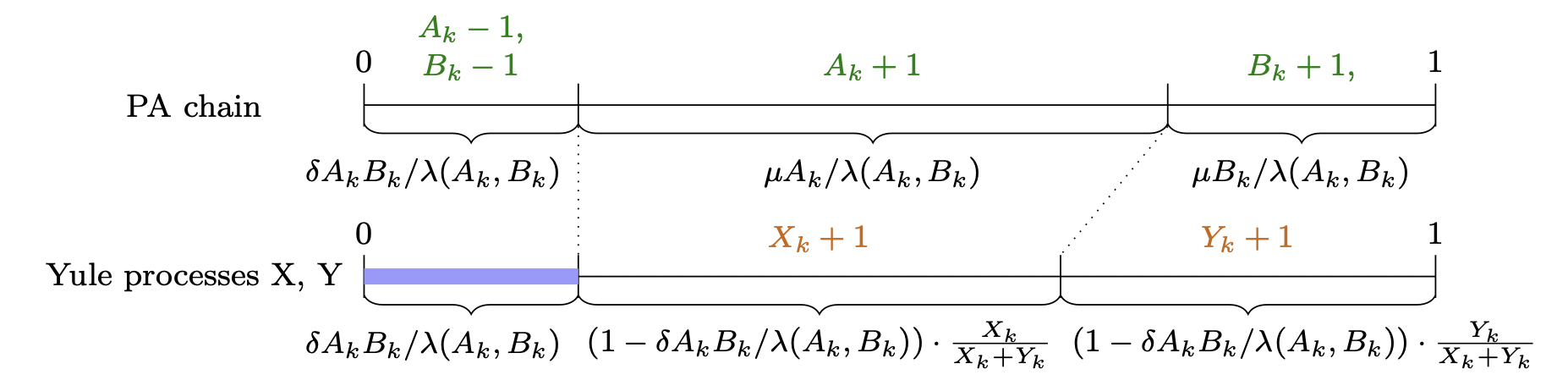
Note that in the coupling "stuttering steps" for $(A_k,B_k)$ or $M_k$ are possible in the definition of the coupled process,
making the underlying discrete-time jump chains of, e.g., chain $(A(t),B(t))$ and the Pairwise Annihilation protocol, potentially differ.
Indeed, the event $(A_{k+1},B_{k+1}) = (A_k,B_k)$ is possible with positive probability if $\lambda(A_k,B_k) < \lambda(M_k)$, and $M_{k+1}=M_k$ has positive probability if $\lambda(M_k) < \lambda(A_k,B_k)$.
The following lemma, however, shows that the continuous-time chain $(A(t),B(t))$ and the Pairwise Annihilation protocol chain have identical transition rates, and are thus identically distributed.
Continuous-time coupling of the Pairwise Annihilation (PA) chain and the single-species birth-death M-chain, given that $A_k \leq B_k$, with $\Lambda = \Lambda(A_k,B_k,M_k)$. The intervals for the cases of $\xi_{k+1}$ and their effect on the Pairwise Annihilation chain and the M-chain are shown in green and orange, respectively. Cases that lead to stuttering steps are shown in blue.
Lemma.
Let $T_1,T_2,\dots$ be a sequence of i.i.d. exponential random variables with rate parameter $\lambda$ and let $k$ be an independent geometric random variable with success probability $p$.
Then $T=T_1+\dots+T_k$
is exponentially distributed with rate parameter $p\lambda$.
By construction of the coupled process, the single-species birth-death process $M(t)$ indeed dominates the minimum of the population counts $A(t)$ and $B(t)$ in the following way:
Lemma.
In the coupled process, $\min\{A(t),B(t)\}\leq M(t)$ for all times $t\geq0$.
The lemma allows to compare the probabilities of extinction in the single-species chain and of consensus in the Pairwise Annihilation protocol chain:
Corollary. $\mathbb{P}(M(t) = 0) \leq \mathbb{P}(A(t) = 0 \vee B(t) = 0)$ for all times $t\geq 0$.
It thus suffices to prove bounds on the time until the population goes extinct in the single-species M chain.
For that, we leverage known results on birth-death processes, which are not applicable to the two-species Pairwise Annihilation protocol chain.
Lemma. If $T$ denotes the time until extinction in the single-species process $M(t)$, then
$\mathbb{E}\,T = O(1)$.
Proof. The birth rate in state $M(t) = i$
is equal to $\alpha(i) = i\mu$ and the death rate is equal to $\beta(i) = i^2 \delta$.
From known general results on birth-death process we obtain,
when starting from initial population $M(0) = M$, that
\begin{equation}
\begin{split}
\mathbb{E}\,T
& =
\sum_{j=1}^M \sum_{k=j-1}^\infty \frac{\alpha(j)\cdots \alpha(k)}{\beta(j)\cdots \beta(k)}\cdot \frac{1}{\beta(k+1)}\\
&=
\sum_{j=1}^M \sum_{k=j-1}^\infty \frac{\mu^{k-j+1}}{\delta^{k-j+1}k!/(j-1)!}\cdot\frac{1}{(k+1)^2\delta}
\end{split}
\end{equation}
Setting $\alpha = \mu/\delta$, we have
\begin{equation}
\begin{split}
\mathbb{E}\,T
& =
\frac{1}{\delta}
\sum_{j=1}^M \sum_{k=j-1}^\infty
\alpha^{k-j+1}
\frac{(j-1)!}{(k+1)!(k+1)}\\
&=
\frac{1}{\delta}
\sum_{j=1}^M
\frac{(j-1)!}{\alpha^{j}}
\sum_{k=j}^\infty
\frac{\alpha^{k}}{k!k}
\\ & =
\frac{1}{\delta}
\sum_{j=1}^M
\frac{(j-1)!}{\alpha^{j}} \cdot
\frac{\alpha^{j}}{j!j}\sum_{k=j}^\infty
\frac{\alpha^{k-j}}{k!/j! \cdot k/j}\\
&\leq
\frac{1}{\delta}
\sum_{j=1}^M
\frac{(j-1)!}{\alpha^{j}} \cdot
\frac{\alpha^{j}}{j!j}\sum_{k=j}^\infty
\frac{\alpha^{k-j}}{(k-j)!}
\end{split}
\end{equation}
since for $k \ge j \ge 1$, it is $k!/j! \ge (k-j)!$ and $k/j \ge 1$.
Thus,
\begin{equation}
\begin{split}
\mathbb{E}\,T & \leq
\frac{1}{\delta}
\sum_{j=1}^M
\frac{(j-1)!}{\alpha^{j}} \cdot
\frac{\alpha^{j}}{j!j} \cdot
e^{\alpha}\\
& =
\frac{e^{\alpha}}{\delta}
\sum_{j=1}^M \frac{1}{j^2}\\
& \leq \frac{e^{\alpha}\pi^2}{6\delta} =
O(1)
\enspace.
\end{split}
\end{equation}
This concludes the proof.
Denoting with $T_{AB}$ the earliest time $t$ such that $A(t)=0$ or $B(t) = 0$, and with $T_M$ the earliest time $t$ such that $M(t) = 0$, the Corollary is equivalent to the inequality
$\mathbb{P}(T_M \leq t ) \leq \mathbb{P}(T_{AB} \leq t)$, which, in turn, is equivalent to the inequality
$\mathbb{P}(T_M > t ) \geq \mathbb{P}(T_{AB} > t)$.
Using the formula $\mathbb{E}\,T = \int_0^\infty \mathbb{P}(T > t)\, dt$, we further have
\begin{equation}
\begin{aligned}
\mathbb{E}\,T_M &= \int_0^\infty \mathbb{P}(T_M > t)\, dt
\\&
\geq \int_0^\infty \mathbb{P}(T_{AB} > t)\, dt
= \mathbb{E}\,T_{AB}\enspace.
\end{aligned}
\end{equation}
This then shows that the expected time until consensus in the Pairwise Annihilation protocol is also $O(1)$.
For the high-probability result, we simply make $\Theta(\log n)$ consecutive tries to achieve extinction in an interval of constant time:
Lemma. If $T$ denotes the time until extinction in the singles-species process $M(t)$, then there exists a constant $C$ such that $\mathbb{P}(T \leq C\log_2 n) = 1 - O(1/n)$.
Proof.
Let $C_1$ be the $O(1)$ constant for the expected value of $T$ and set $C=\max\{2C_1,2\}$.
Then, by Markov's inequality, we have
$\mathbb{P}(T > C) \leq C_1/C \leq 1/2$.
Thus, the probability of the event $T > C\log_2 n$ is dominated by the probability of failing $\log_2 n$ consecutive tries with a Bernoulli random variable with parameter $p = 1/2$.
But this probability is $2^{-\log_2 n} = 1/n$.